Consider first a continuous random variable ![]() having probability
density function of the following form
having probability
density function of the following form
| (1) |
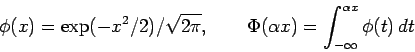 |
(2) |
The density ![]() enjoys various interesting formal properties.
It is easy to check that
enjoys various interesting formal properties.
It is easy to check that
The above random variable ![]() and its density function
and its density function ![]() are the basic components of the construct, but for practical
numerical work we need to add location and scale parameters.
Consider then the linear transform
are the basic components of the construct, but for practical
numerical work we need to add location and scale parameters.
Consider then the linear transform
| (3) |
| (4) |
We refer to
![]() ,
, ![]() and
and ![]() as the location, the scale and the shape parameters, respectively.
Notice that, when
as the location, the scale and the shape parameters, respectively.
Notice that, when ![]() , we re-obtain the
, we re-obtain the
![]() distribution.
You can see additional plots, varying all three parameters,
with a demostration program which produces graphs of the
univariate skew-normal densities.
distribution.
You can see additional plots, varying all three parameters,
with a demostration program which produces graphs of the
univariate skew-normal densities.
Some characteristic values of the random variable ![]() are as follows:
are as follows:
| mean value |
|
|
| variance |
|
|
| skewness |
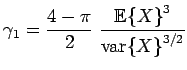 |
|
| kurtosis |
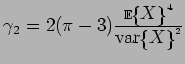 |
On the statistical side, the skew-normal distribution is often useful to fit observed data with "normal-like" shape of the empirical distribution but with lack of symmetry. You can try it out directly with your data using a form available here.
Ok, but why is it called skew-normal? One reason is implicit
in the above passage: this family of distributions includes the
standard N(0,1) distribution as a special case,
but in general its memebers have a skewed density.
Another appealing connection is the fact that
| (5) |
So far for the univariate distribution; a multivariate
version also exists. This refers to a multivariate variable ![]() such that
such that
The present account of the skew-normal distribution is clearly extremely limited. For an extended treatment, see the proper publications.
Back to the Skew-normal distribution